The number zero is an annoying and dangerous beast. It should be abolished.

Copyright Married to the Sea. Reproduced here by permission.
The number zero hasn’t always been with us. For thousands of years – millions – we got along without it. It’s true that some calculations are more difficult without it. Try multiplying Roman numerals, for example. V x VI = XXX? There wasn’t much you could do about it back then.
The first use of zero was apparently by an Indian mathematician named Brahmagupta, who was born about 600 C.E. He conceived the notion that some quantity, minus itself, must equal a number. That number was zero. It doesn’t sound like a big deal, but it was innovative in its time – to treat “nothing” as just another number. Note that zero isn’t actually “nothing.” If you have ten each of apples and oranges, and take 10 apples away, you have zero apples – but you still have oranges. You’re not left with nothing.
Zero has its uses. In our way or representing numbers, zero is a placeholder for empty numbers. We know that 1000 is bigger than 100, because of the zeroes. The more zeroes after a number, the bigger it is. So on a paycheck, zeroes are OK.
The Malignity of the Number Zero Rears Its Offensive Head
Ah, but there is a fly in the ointment, one little property that zero has, that no other number does. This unique property should make us suspicious. You can’t divide with it. This fact was glossed over when they taught us how to calculate. We learned how to multiply, divide, add, and subtract any numbers with any others – except, we cannot divide by zero.
Division by zero is considered “undefined.” It’s not infinity, though it’s often said to be. It’s undefined. Division by zero has no meaning in mathematics, neither number nor infinity nor anything else. Undefined. It’s the only number that behaves this way. Out of the infinitudes of numbers, countable and uncountable, natural, integer, real, complex, transcendental, and whatever other kinds there are, only one number can’t divide into another. Zero.
Does anyone have a problem with this? Apparently not. Mathematicians seem OK with it, accountants, everyone else. Well, almost…
I said mathematicians are OK with zero, but that’s not quite true. Throughout all of mathematics, zero lurks around and bites mathematicians right in the asymptote if they’re not careful. You can’t use the logarithm of zero, because that involves a division by zero. You can’t take the tangent of 90° for the same reason. You have to watch out with your equations to make sure nothing can ever equate to dividing by zero. So you have an equation like 1/(X-1), where X can have any value – oh, except for 1. If X = 1, then X-1 = 0, and you can’t divide by zero. So if you get an equation like this, you have to qualify it by saying, “X ≠ 1.” That is, X is not equal to one.
The Theory of Limits
There is another place where zero gives trouble, but this also appears to have been glossed over somewhat. It’s the concept of limits. Take the simple series of fractions: 1/2 + 1/4 + 1/8 + … (The three dots indicate that this series goes on forever). You keep doubling the bottom number (the denominator). You can take this out as far as you want. Each new term (fraction) is half the previous one. As you can imagine, the numbers get small very quickly. After a few dozen terms the numbers are almost zero – but not quite. They’ll never be zero, no matter how many times you repeat this process.
Since we’re adding all these terms, and we’re summing an infinite number of terms, you’d think that the sum would be infinity. It’s not. Believe it or not, the sum never exceeds 1. In fact, the sum never reaches 1 in any finite number of steps. The number 1 is said to be the limit of the series as the number of terms approaches infinity. The idea is that if you somehow could add up all the infinite number of terms, the sum would add up to exactly one. But you can’t add up an infinite number of terms. And for any finite number of terms, that last term never equals zero.
The way mathematicians get around this is to say that the series approaches 1 as closely as you want. Pick a number less than 1 – say, 0.99. That’s pretty close to 1. If you add up enough of those terms, you’ll get a number that’s closer to 1 than that. No matter how close a number you pick, the series can come even closer. It’s almost as if the last term really becomes zero – but of course, it doesn’t. The last term is never zero.
In this series, the limit is said to be 1. It will never be greater than 1. Personally, I don’t think mathematicians have shown that it ever reaches 1. Common sense says it must be so – in some ways, it’s “obvious.” But is it mathematically true?
The concept of limits is vital to mathematics. It’s the basis of much of the calculus, for example. For hundreds of years the concept of limits has been used successfully to prove many important theorems in mathematics – which in turn has helped advance science – in particular, theoretical physics. Calculating orbits, the trajectories of satellites, how stars and molecules move, how to build bridges and skyscrapers, all rely on concepts based on limits. Our rockets fly (more or less), eclipses and planets move according to our predictions, and everyone’s happy. Except me.

Actually a few others have had their doubts about limits. Niels H. Abels said:
If you disregard the very simplest cases, there is in all of mathematics not a single infinite series whose sum has been rigorously determined. In other words, the most important parts of mathematics stand without a foundation.

Another mathematician, Bishop George Berkeley wrote:
And what are these same evanescent Increments? They are neither finite Quantities, nor Quantities infinitely small, nor yet nothing. May we not call them the Ghosts of departed Quantities?
I like that guy. Too bad he died in 1783. I can’t really count on him for backup.
Yet Another Problem
The notion of limits might almost be acceptable, except for two concepts called supremum and infimum. The mathematical definitions of these words are tiresome, so I’ll skip all that and present an example, which would concern the supremum:
Consider what’s the biggest number that’s still less than a given number, say 1. That’s the supremum. If we’re talking about integers (whole numbers), then that number is 0. There is no integer greater than 0 that is also less than 1. If we’re talking about numbers with decimal places, like 0.99, it’s not possible to give an answer. No matter what number you choose, I can name another number that’s bigger, but still less than 1. If you say 0.9, I’ll say 0.99. If you say 0.99, I’ll say 0.999. And so on. I can always tack on another 9 at the end and get a larger number that’s still less than 1.
Does this look familiar? It’s the same idea as limits. You can approach 1 as closely as you like, so the limit of this procedure is 1. But we’re looking for a number that’s less than 1. Now we’ve got a problem.
Mathematicians avoid this whole mess by simply saying that this number doesn’t exist. Problem solved. Personally I think that’s cheating.
Still, there’s a glimmer of hope for me in physics. Here is where things actually get interesting. Physicists don’t believe in zero, at least as far as its having a physical meaning. It’s something of a long story…
The Ultraviolet Catastrophe
About 100 years ago, physicists were faced with a serious problem concerning black body radiation. A “black body” is a theoretical object that perfectly absorbs or emits energy (called radiation). Practical (imperfect) black bodies were heated until they glowed. Measurements were taken of the different colors of light emitted at different temperatures. The data was plotted onto graphs, which looked like this:
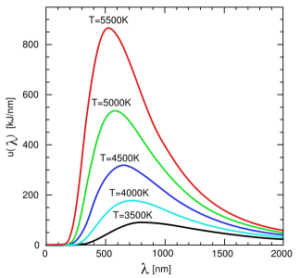
Graph of Black Body Data As Measured
This doesn’t hold any surprises. You perform an experiment, get the results, plot them, and have a nice graph. You can see how the lines start out low, rise, reach a maximum, and go back down again. This is the graph they got from their labs.
There was a classic physics equation that predicted what the curve should look like for different temperatures. It worked reasonably well for the lower temperatures, giving about the same curve as they got in the labs. The equation failed miserably when applied to the higher temperatures. The equation should have produced the same graph as the lab results did. Unfortunately, its graph looked like this:
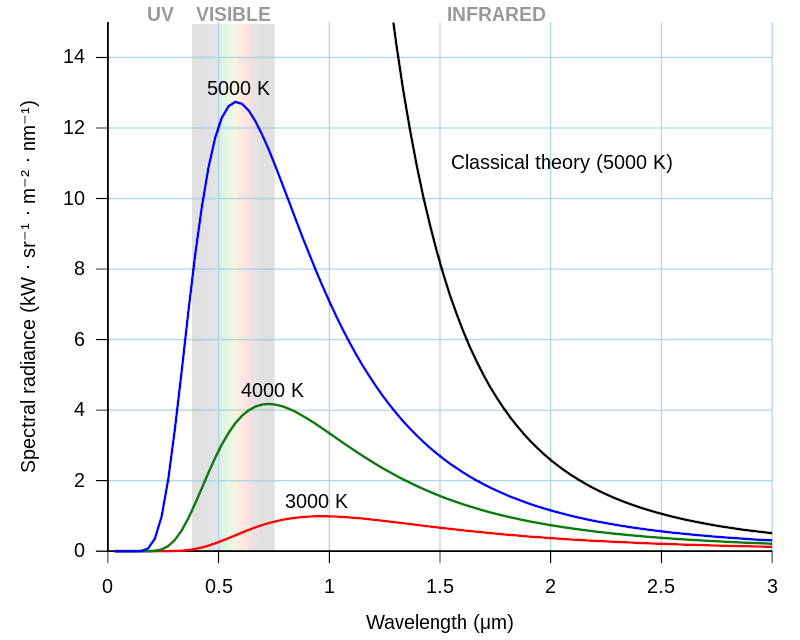
Graph of Black Body Radiation As Calculated
You can see that some of the curves just run right off the graph. Those were the ones for the higher temperatures. At high temperatures – towards the ultraviolet – the calculated energy was enormous, approaching infinity. This was a serious problem because the equation was fundamental.
The crux of the problem is that the equation was a fraction, and the denominator could approach zero. As the temperature increases, the denominator gets smaller, and the calculated energy becomes ridiculously high – far beyond what was found in the labs. According to the equation, a body should radiate an infinite amount of energy. This made a lot of people very unhappy.
The Ultraviolet Catastrophe was one of the problems in classical physics that led to the quantum theory. Max Planck, while working on a different problem, had the idea that the wavelengths of light could never reach zero, could never fall below some number. Planck considered this a convenient fiction, but when he used it in his equations, many problems disappeared and the equations started giving correct results. He called this minimum wavelength a quantum, which means a quantity or amount.

There was no mathematical justification for this move. He didn’t arrive at it through careful calculations. He simply made it a requirement. Despite its lack of foundation, the idea worked beautifully. Eventually the notion of quanta was applied to the Ultraviolet Catastrophe problem. This led to equations that yielded curves in agreement with experiment.
There was much furor over this and other quantum ideas. There really was no mathematical or theoretical justification for requiring energy or matter to exist in ‘quanta’. It just worked. This is fine in engineering, but it’s not so great in theoretical physics. Einstein, whose work helped to start the quantum revolution, spent the rest of his life trying to disprove it. Many classical physicists were outraged over this seemingly ad hoc solution. No one was very happy about it, but it kept yielding stunning, accurate results. Most physicists decided that you can’t argue with success, and accepted the quantum theory uneasily.

Werner Heisenberg was an early quantum theorist who developed the Uncertainty Principle. There are several ways of expressing this non-mathematically, but the gist of it is that you can’t know the precise location of a particle, and at the same time know its precise momentum (or motion). The more you know about one, the less you know about the other, and you can’t know either one exactly. There’s always a minimum error.
One consequence of the Uncertainty Principle is that you can’t say that any region of space is empty. In fact, there is a phenomenon known as “quantum space” or “quantum foam” in which particles continually pop into existence and wink out almost immediately. Empty space isn’t empty after all – it’s boiling with “virtual particles.” Meaning, there’s nowhere that there are zero particles. No truly empty space. No zero.
The consequences of this notion of quanta are far-reaching. There are certain physical units called “Planck Units” that represent the minimum meaningful value for certain physical properties. For instance, there is the Planck Length, which is about 1.6 x 10-35 meters; Planck Time, which is 5.4 x 10-44 seconds; and so on. These are incredibly tiny values, irrelevant for almost all purposes. They’re the smallest possible values for these properties. You can’t say that something is shorter than the Planck Length. Speaking of zero length or zero time is physically meaningless.
This means that we don’t have situations in which zero occurs to mess up our equations. We can’t divide by zero because zero has no physical meaning. This is a Good Thing™.
So quantum theory has spared me from the ravages of the number zero.
